Histoires de Mathématiques
Programmes d'enseignement
Ce qui suit est extrait des programmes de mathématiques pour les différents niveaux, disponibles sur le site éduscol du Ministère de l'Éducation Nationale et de la Jeunesse (au 1er septembre 2020). Pour les cycles 2, 3, 4, les têtes de chapitre sont celles des Repères Annuels de Progression. Pour les classes de seconde, première et terminale, les paragraphes intitulés Histoire des Mathématiques ont été extraits des programmes en vigueur. L'objectif est de relier les programmes au contenu de ce site.
Cycle 2 ►
Nombres et calculs
Nombres Origine de la numération
Origine de la numération
 École de scribes à Nippur
École de scribes à Nippur
 Arithmétique en Égypte
Arithmétique en Égypte
 Aristote et l'arithmétique
Aristote et l'arithmétique
 Histoire du zéro
Histoire du zéro
 Boèce et ses mathématiques
Boèce et ses mathématiques
 Gerbert, savant et pape
Gerbert, savant et pape
 Arithmétique des Incas et des Mayas
Arithmétique des Incas et des Mayas
Résolution de problèmes
 Poètes et mathématiciens en Inde
Poètes et mathématiciens en Inde
 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Alcuin, savant de Charlemagne
Alcuin, savant de Charlemagne
 Récréations mathématiques
Récréations mathématiques
Calcul
 Machine d'Anticythère
Machine d'Anticythère
 Anciennes méthodes pour compter
Anciennes méthodes pour compter
 Progressions geometriques
Progressions geometriques
Grandeurs et mesures
Longueur masse contenance Astronomie et astrologie en Grèce
Astronomie et astrologie en Grèce
 Géométrie et astronomie en Grèce
Géométrie et astronomie en Grèce
 Flocon de neige de Kepler
Flocon de neige de Kepler
 Étatisme et statistique
Étatisme et statistique
 Victoire du système décimal
Victoire du système décimal
 Épopée du mètre-étalon
Épopée du mètre-étalon
Durées
 Astronomie mésopotamienne
Astronomie mésopotamienne
 Instruments astronomiques
Instruments astronomiques
 Victoire du système décimal
Victoire du système décimal
 Détermination des longitudes
Détermination des longitudes
Prix
 Arithmétiques commerciales
Arithmétiques commerciales
Espace et géométrie
Se repérer et se déplacer en utilisant des repères et des représentations Astronomie et astrologie en Grèce
Astronomie et astrologie en Grèce
 Géodésiens alpinistes
Géodésiens alpinistes
 Détermination des longitudes
Détermination des longitudes
Reconnaître, nommer, décrire, reproduire quelques solides
 Flocon de neige de Kepler
Flocon de neige de Kepler
 Coniques d'Apollonius
Coniques d'Apollonius
 Polyèdres réguliers
Polyèdres réguliers
 Probabilités et problème des partis
Probabilités et problème des partis
Reconnaître, nommer, décrire, reproduire, construire quelques figures géométriques
 Pi avant Archimède
Pi avant Archimède
 Éléments d'Euclide et enseignement
Éléments d'Euclide et enseignement
 Le
tangram d'Archimède
Le
tangram d'Archimède
 Pavages de Truchet
Pavages de Truchet
 Quadrateurs de cercle
Quadrateurs de cercle
 Pavages d'Escher
Pavages d'Escher
Reconnaître et utiliser les notions d'alignement, d'angle droit, d'égalité de longueurs, de milieu, de symétrie
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Habillages du théorème de Pythagore
Habillages du théorème de Pythagore
 Le tangram d'Archimède
Le tangram d'Archimède
 Pavages de Truchet
Pavages de Truchet
 Sangakus et cercles tangents
Sangakus et cercles tangents
 Pavages d'Escher
Pavages d'Escher
Cycle 3 ►
Nombres et calculs
Les nombres entiers Origine de la numération
Origine de la numération
 École de scribes à Nippur
École de scribes à Nippur
 Aristote et l'arithmétique
Aristote et l'arithmétique
 Histoire du zéro
Histoire du zéro
 Lecture des grands nombres
Lecture des grands nombres
 Triplets pythagoriciens
Triplets pythagoriciens
 Arithmétique des Incas et des Mayas
Arithmétique des Incas et des Mayas
Fractions
 Arithmétique en Égypte
Arithmétique en Égypte
 Poètes et mathématiciens en Inde
Poètes et mathématiciens en Inde
 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Gerbert, savant et pape
Gerbert, savant et pape
 Alcuin, savant de Charlemagne
Alcuin, savant de Charlemagne
Nombres décimaux
 Victoire du système décimal
Victoire du système décimal
Calcul
 Anciennes méthodes pour compter
Anciennes méthodes pour compter
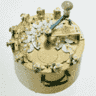 Machines à calculer
Machines à calculer
 Oughtred et la règle à calcul
Oughtred et la règle à calcul
La résolution de problèmes
 École de scribes à Nippur
École de scribes à Nippur
 Arithmétique en Égypte
Arithmétique en Égypte
 Boèce et ses mathématiques
Boèce et ses mathématiques
 Progressions geometriques
Progressions geometriques
 Gerbert, savant et pape
Gerbert, savant et pape
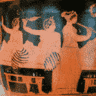 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Poètes et mathématiciens en Inde
Poètes et mathématiciens en Inde
Grandeurs et mesures
Les longueurs Pi avant Archimède
Pi avant Archimède
 Astronomie et astrologie en Grèce
Astronomie et astrologie en Grèce
 Géométrie et astronomie en Grèce
Géométrie et astronomie en Grèce
 Lunules d'Hippocrate
Lunules d'Hippocrate
 Quadrateurs de cercle
Quadrateurs de cercle
Les durées
 Astronomie mésopotamienne
Astronomie mésopotamienne
 Zodiaque de Dendérah
Zodiaque de Dendérah
 Victoire du système décimal
Victoire du système décimal
 Détermination des longitudes
Détermination des longitudes
 Astronomie indienne
Astronomie indienne
Les aires
 Pi avant Archimède
Pi avant Archimède
 Algèbre et géométrie en Mésopotamie
Algèbre et géométrie en Mésopotamie
 Le tangram d'Archimède
Le tangram d'Archimède
Les contenances et les volumes
 Flocon de neige de Kepler
Flocon de neige de Kepler
 Kepler et le calcul intégral
Kepler et le calcul intégral
 Quadratures d'Archimède
Quadratures d'Archimède
 Pascal et la cycloïde
Pascal et la cycloïde
Les angles
 Le tangram d'Archimède
Le tangram d'Archimède
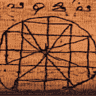 Premières tables trigonométriques
Premières tables trigonométriques
 Géométrie des alvéoles d'abeilles
Géométrie des alvéoles d'abeilles
 Pavages d'Escher
Pavages d'Escher
 Florence Nightingale et les maladies infectieuses
Florence Nightingale et les maladies infectieuses
Proportionnalité
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Théorème de Merton et mouvement accéléré
Théorème de Merton et mouvement accéléré
Espace et géométrie
Les apprentissages spatiaux Géodésiens alpinistes
Géodésiens alpinistes
 Épopée du mètre-étalon
Épopée du mètre-étalon
Initiation à la programmation
 Triangle de Pascal
Triangle de Pascal
 Pavages de Truchet
Pavages de Truchet
Les apprentissages géométriques
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Pi avant Archimède
Pi avant Archimède
 Polyèdres réguliers
Polyèdres réguliers
 Coniques d'Apollonius
Coniques d'Apollonius
 Le tangram d'Archimède
Le tangram d'Archimède
 Probabilités et problème des partis
Probabilités et problème des partis
 Pavages de Truchet
Pavages de Truchet
 Pavages d'Escher
Pavages d'Escher
 Quadrateurs de cercle
Quadrateurs de cercle
Le raisonnement
 Démonstrations du théorème de Pythagore
Démonstrations du théorème de Pythagore
 Éléments d'Euclide et enseignement
Éléments d'Euclide et enseignement
 Géométrie hyperbolique
Géométrie hyperbolique
 Somme des angles d'un triangle
Somme des angles d'un triangle
Le vocabulaire et les notations
 Notations algébriques
Notations algébriques
Les instruments
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Lunules d'Hippocrate
Lunules d'Hippocrate
 Instruments astronomiques
Instruments astronomiques
 Géométrie du compas seul
Géométrie du compas seul
 Solution des trois problèmes grecs
Solution des trois problèmes grecs
La symétrie axiale
 Polyèdres réguliers
Polyèdres réguliers
 Pavages de Truchet
Pavages de Truchet
 Pavages d'Escher
Pavages d'Escher
 Éléments d'Euclide et enseignement
Éléments d'Euclide et enseignement
 Le tangram d'Archimède
Le tangram d'Archimède
La proportionnalité
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Géométrie et perspective
Géométrie et perspective
Cycle 4 ►
Nombres et calculs
Nombres décimaux relatifs Al-Khwarizmi et l'algèbre
Al-Khwarizmi et l'algèbre
 Notations algébriques
Notations algébriques
Fractions, nombres rationnels
 Arithmétique en Égypte
Arithmétique en Égypte
 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Victoire du système décimal
Victoire du système décimal
 Astronomie indienne
Astronomie indienne
Racine carrée
 Poètes et mathématiciens en Inde
Poètes et mathématiciens en Inde
 Calculs de racines
Calculs de racines
 Habillages du théorème de Pythagore
Habillages du théorème de Pythagore
Puissances
 Progressions geometriques
Progressions geometriques
 Paradoxes de Zénon et séries géométriques
Paradoxes de Zénon et séries géométriques
 Napier et les logarithmes
Napier et les logarithmes
 Lecture des grands nombres
Lecture des grands nombres
Divisibilité, nombres premiers
 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Arithmétique arabe
Arithmétique arabe
 Gauss et l'arithmétique complexe
Gauss et l'arithmétique complexe
 Hadamard, Erdös et les nombres premiers
Hadamard, Erdös et les nombres premiers
Calcul littéral
 Arithmétiques de Diophante
Arithmétiques de Diophante
 Algèbre indienne
Algèbre indienne
 Notations algébriques
Notations algébriques
 Algebre de Bombelli
Algebre de Bombelli
 Harriot entre Viète et Descartes
Harriot entre Viète et Descartes
Équations
 Algèbre et géométrie en Mésopotamie
Algèbre et géométrie en Mésopotamie
 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Systèmes d'équations en Chine
Systèmes d'équations en Chine
 Algèbre indienne
Algèbre indienne
 Al-Khwarizmi et l'algèbre
Al-Khwarizmi et l'algèbre
 Omar Khayyam
Omar Khayyam
 Équations de degré trois
Équations de degré trois
Organisation et gestion de données, fonctions
Statistiques Statistiques démographiques
Statistiques démographiques
 Étatisme et statistique
Étatisme et statistique
 Playfair et les graphiques statistiques
Playfair et les graphiques statistiques
 Florence Nightingale et les maladies infectieuses
Florence Nightingale et les maladies infectieuses
 Semmelweis et la fièvre puerpérale
Semmelweis et la fièvre puerpérale
 Statistiques selon Dupin
Statistiques selon Dupin
 D'Angeville et la statistique non paramétrique
D'Angeville et la statistique non paramétrique
Probabilités
 Probabilités et jeux de dés
Probabilités et jeux de dés
 Probabilités et problème des partis
Probabilités et problème des partis
 Premier test statistique
Premier test statistique
 Probabilités géométriques
Probabilités géométriques
Proportionnalité
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Lunules d'Hippocrate
Lunules d'Hippocrate
Fonctions
 Astronomie mésopotamienne
Astronomie mésopotamienne
 Oresme et la représentation des fonctions
Oresme et la représentation des fonctions
Grandeurs et mesures
Calculs sur des grandeurs mesurables Algèbre et géométrie en Mésopotamie
Algèbre et géométrie en Mésopotamie
 Pi avant Archimède
Pi avant Archimède
 Le tangram d'Archimède
Le tangram d'Archimède
 Flocon de neige de Kepler
Flocon de neige de Kepler
 Quadratures d'Archimède
Quadratures d'Archimède
 Kepler et le calcul intégral
Kepler et le calcul intégral
Effet des transformations sur des grandeurs géométriques
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Klein et son programme d'Erlangen
Klein et son programme d'Erlangen
Représenter l'espace
 Coniques d'Apollonius
Coniques d'Apollonius
 Géométrie et perspective
Géométrie et perspective
 Descartes, Fermat et les coordonnées
Descartes, Fermat et les coordonnées
 Desargues et la géométrie projective
Desargues et la géométrie projective
 Géométrie de Monge
Géométrie de Monge
 Géométrie projective de Poncelet
Géométrie projective de Poncelet
Géométrie plane (Figures et configurations, Transformations)
 Théorème de Thalès et applications
Théorème de Thalès et applications
 Lunules d'Hippocrate
Lunules d'Hippocrate
 Éléments d'Euclide et enseignement
Éléments d'Euclide et enseignement
 Le tangram d'Archimède
Le tangram d'Archimède
 Représentation géométrique des complexes
Représentation géométrique des complexes
Algorithmique et programmation
Écrire, mettre au point, exécuter un programme Recettes, algorithmes et mathématiques
Recettes, algorithmes et mathématiques
 Calculs de racines
Calculs de racines
 Cheminement du mot algorithme
Cheminement du mot algorithme
 Comput pascal
Comput pascal
 La vision d'Ada Lovelace
La vision d'Ada Lovelace
 Calcul au début des ordinateurs
Calcul au début des ordinateurs
Seconde ►
Nombres et calculs
La notion apparemment familière de nombre ne va pas de soi.
Deux exemples : la crise provoquée par la découverte des irrationnels
chez les mathématiciens
grecs
 Scandale des irrationnelles,
la différence entre « nombres réels »
et « nombres de la
calculatrice »
Scandale des irrationnelles,
la différence entre « nombres réels »
et « nombres de la
calculatrice »
 Victoire du système décimal.
Il s'agit également de souligner
le gain en efficacité et en généralité qu'apporte le calcul
littéral
Victoire du système décimal.
Il s'agit également de souligner
le gain en efficacité et en généralité qu'apporte le calcul
littéral
 Notations algébriques
Notations algébriques
 Algèbre indienne
Algèbre indienne
 Al-Khwarizmi et l'algèbre,
en expliquant qu'une grande partie des mathématiques n'a pu se
développer qu'une fois ce formalisme stabilisé au cours des siècles.
Il est possible d'étudier des textes anciens d'auteurs tels que
Diophante
Al-Khwarizmi et l'algèbre,
en expliquant qu'une grande partie des mathématiques n'a pu se
développer qu'une fois ce formalisme stabilisé au cours des siècles.
Il est possible d'étudier des textes anciens d'auteurs tels que
Diophante
 Arithmétiques de Diophante,
Euclide
Arithmétiques de Diophante,
Euclide
 Éléments d'Euclide et enseignement,
Al-Khwarizmi
Éléments d'Euclide et enseignement,
Al-Khwarizmi
 Al-Khwarizmi et l'algèbre,
Fibonacci
Al-Khwarizmi et l'algèbre,
Fibonacci
 Fibonacci et l'arithmétique,
Viète
Fibonacci et l'arithmétique,
Viète
 Viète, cryptographie et algèbre,
Fermat
Viète, cryptographie et algèbre,
Fermat
 Fermat et l'arithmétique
Fermat et l'arithmétique
 Optimisation selon Fermat,
Descartes
Optimisation selon Fermat,
Descartes
 Descartes, Fermat et les coordonnées
Descartes, Fermat et les coordonnées
 Tourbillons de Descartes
et mettre en évidence leurs aspects algorithmiques.
Tourbillons de Descartes
et mettre en évidence leurs aspects algorithmiques.
Géométrie
Les progrès apportés par la « méthode des coordonnées »
de Descartes
 Coniques d'Apollonius
Coniques d'Apollonius
 Descartes, Fermat et les coordonnées,
puis par la notion de
vecteur
Descartes, Fermat et les coordonnées,
puis par la notion de
vecteur
 Grassmann et les vecteurs, permettent
de relier efficacement géométrie, physique et calcul.
On pourra évoquer les mathématiques
grecques
Grassmann et les vecteurs, permettent
de relier efficacement géométrie, physique et calcul.
On pourra évoquer les mathématiques
grecques
 Éléments d'Euclide et enseignement,
en mettant en évidence
le rôle central de la géométrie dans la naissance de l'idée de
démonstration
Éléments d'Euclide et enseignement,
en mettant en évidence
le rôle central de la géométrie dans la naissance de l'idée de
démonstration
 Lunules d'Hippocrate
Lunules d'Hippocrate
 Le tangram d'Archimède
ainsi que le faible développement de l'algèbre
sous
l'Antiquité
Le tangram d'Archimède
ainsi que le faible développement de l'algèbre
sous
l'Antiquité
 Algèbre et géométrie en Mésopotamie
Algèbre et géométrie en Mésopotamie
 Arithmétiques de Diophante,
en partie dû à l'appui systématique sur la géométrie.
Arithmétiques de Diophante,
en partie dû à l'appui systématique sur la géométrie.
Fonctions
On peut évoquer la très lente élaboration de la notion de
fonction
 Oresme et la représentation des fonctions,
depuis l'Antiquité
Oresme et la représentation des fonctions,
depuis l'Antiquité
 Astronomie mésopotamienne
jusqu'à la codification actuelle par Dirichlet,
en mettant en évidence quelques étapes importantes :
Newton
Astronomie mésopotamienne
jusqu'à la codification actuelle par Dirichlet,
en mettant en évidence quelques étapes importantes :
Newton
 Newton et l'analyse infinitésimale,
Leibniz
Newton et l'analyse infinitésimale,
Leibniz
 Newton contre Leibniz,
Euler
Newton contre Leibniz,
Euler
 Euler et l'analyse.
On souligne alors l'importance de la notation algébrique
Euler et l'analyse.
On souligne alors l'importance de la notation algébrique
 Cordes vibrantes.
Cordes vibrantes.
Statistique et probabilités
L'histoire des probabilités fournit un cadre pour dégager les éléments
de la mathématisation du hasard. Un exemple est le problème des
partis
 Probabilités et problème des partis,
dit aussi du chevalier de Méré, l'échange de lettres entre Pascal et
Fermat sur ce point puis les travaux de Pascal, Fermat et Huygens
qui en découlent. Le problème du duc de
Toscane
Probabilités et problème des partis,
dit aussi du chevalier de Méré, l'échange de lettres entre Pascal et
Fermat sur ce point puis les travaux de Pascal, Fermat et Huygens
qui en découlent. Le problème du duc de
Toscane
 Probabilités et jeux de dés
ou les travaux de
Leibniz sur le jeu de dés peuvent aussi être évoqués.
Probabilités et jeux de dés
ou les travaux de
Leibniz sur le jeu de dés peuvent aussi être évoqués.
Algorithmique et programmation
De nombreux textes témoignent d'une préoccupation algorithmique au long de l'Histoire Recettes, algorithmes et mathématiques.
Lorsqu'un texte historique a une visée
algorithmique
Recettes, algorithmes et mathématiques.
Lorsqu'un texte historique a une visée
algorithmique
 Arithmétique en Égypte
Arithmétique en Égypte
 Calculs de racines
Calculs de racines
 Triangle de Pascal
Triangle de Pascal
 Cheminement du mot algorithme
Cheminement du mot algorithme
 Comput pascal
transformer les méthodes qu'il présente en un algorithme, voire en un
programme, ou inversement, est l'occasion de travailler des changements
de registre qui donnent du sens au formalisme mathématique.
Comput pascal
transformer les méthodes qu'il présente en un algorithme, voire en un
programme, ou inversement, est l'occasion de travailler des changements
de registre qui donnent du sens au formalisme mathématique.
Première ►
Algèbre
Bien avant de faire l'objet d'une étude formalisée, les suites
apparaissent dans deux types de situations :
l'approximation de nombres réels (encadrement de pi par
Archimède
 Pi avant Archimède,
calcul de la racine carrée chez Héron
d'Alexandrie
Pi avant Archimède,
calcul de la racine carrée chez Héron
d'Alexandrie
 Calculs de racines)
et les
problèmes de comptage (les lapins de
Fibonacci
Calculs de racines)
et les
problèmes de comptage (les lapins de
Fibonacci
 Fibonacci et l'arithmétique, etc.).
Fibonacci et l'arithmétique, etc.).
Les problèmes décrits dans les livres de Fibonacci, ou chez les savants
arabes qui le précèdent, se modélisent avec des suites. Oresme calcule
des sommes de termes de suites géométriques au
XIVe
siècle
 Paradoxes de Zénon et séries géométriques
Paradoxes de Zénon et séries géométriques
 Napier et les logarithmes.
On trouve chez Diophante
Napier et les logarithmes.
On trouve chez Diophante
 Arithmétiques de Diophante, puis chez
Al-Khwarizmi
Arithmétiques de Diophante, puis chez
Al-Khwarizmi
 Al-Khwarizmi et l'algèbre,
des méthodes de résolutions d'équations du second
degré
Al-Khwarizmi et l'algèbre,
des méthodes de résolutions d'équations du second
degré
 Algèbre et géométrie en Mésopotamie.
Le travail novateur
d'Al-Khwarizmi reste en partie tributaire de la tradition
(utilisation de considérations géométriques équivalentes à la forme
canonique) et de l'état alors embryonnaire de la notation algébrique,
ainsi que de l'absence des nombres négatifs. Les méthodes actuelles
sont un aboutissement de ce long cheminement vers un formalisme
efficace et
concis
Algèbre et géométrie en Mésopotamie.
Le travail novateur
d'Al-Khwarizmi reste en partie tributaire de la tradition
(utilisation de considérations géométriques équivalentes à la forme
canonique) et de l'état alors embryonnaire de la notation algébrique,
ainsi que de l'absence des nombres négatifs. Les méthodes actuelles
sont un aboutissement de ce long cheminement vers un formalisme
efficace et
concis
 Notations algébriques
Notations algébriques
 Algebre de Bombelli
Algebre de Bombelli
 Stevin, Girard et l'algèbre avant Descartes
Stevin, Girard et l'algèbre avant Descartes
 Harriot entre Viète et Descartes.
Harriot entre Viète et Descartes.
Analyse
Le calcul différentiel s'est imposé par sa capacité à donner des
solutions simples à des problèmes nombreux d'origines variées
(cinématique, mécanique, géométrie, optimisation). Le développement
d'un calcul des variations chez Leibniz et Newton se fonde sur
l'hypothèse que les phénomènes naturels évoluent linéairement
quand on leur applique des petites variations. Leurs approches
partent de notions intuitives mais floues d'infiniment
petit
 Newton et l'analyse infinitésimale
Newton et l'analyse infinitésimale
 Newton contre Leibniz.
Ce n'est que très progressivement que les notions de limites
et de différentielles
Newton contre Leibniz.
Ce n'est que très progressivement que les notions de limites
et de différentielles
 Les Bernoulli et l'analyse
Les Bernoulli et l'analyse
 Oppositions au calcul différentiel,
qui en fondent l'exposé actuel, ont été
clarifiées au XIXe
siècle
Oppositions au calcul différentiel,
qui en fondent l'exposé actuel, ont été
clarifiées au XIXe
siècle
 Bolzano, Cauchy et la rigueur.
Bolzano, Cauchy et la rigueur.
La notation exponentielle et les fonctions exponentielles
apparaissent vers la fin du XVIIe
siècle
 Euler contre Voltaire,
procédant d'une volonté de traiter des phénomènes de croissance
comparables à ceux des intérêts composés. La modélisation de ces
situations fait naturellement apparaître la caractérisation de la
fonction exponentielle comme seule fonction vérifiant l'équation
différentielle y'=y et la condition initiale y(0)=1.
Euler contre Voltaire,
procédant d'une volonté de traiter des phénomènes de croissance
comparables à ceux des intérêts composés. La modélisation de ces
situations fait naturellement apparaître la caractérisation de la
fonction exponentielle comme seule fonction vérifiant l'équation
différentielle y'=y et la condition initiale y(0)=1.
La trigonométrie a été utilisée chez les
Anciens
 Théorème d'al-Kashi
Théorème d'al-Kashi
 Premières tables trigonométriques
Premières tables trigonométriques
 Des cordes à la sinusoïde
dans des problèmes
de natures diverses (géométrie, géographie, astronomie). Elle est à
l'époque fondée sur la fonction
corde
Des cordes à la sinusoïde
dans des problèmes
de natures diverses (géométrie, géographie, astronomie). Elle est à
l'époque fondée sur la fonction
corde
 Histoire du zéro
Histoire du zéro
 Premières tables trigonométriques,
d'un maniement bien moins
facile que les fonctions sinus et cosinus
Premières tables trigonométriques,
d'un maniement bien moins
facile que les fonctions sinus et cosinus
 Des cordes à la sinusoïde
de la présentation actuelle.
Des cordes à la sinusoïde
de la présentation actuelle.
Géométrie
La notion de vecteur était implicite en mécanique depuis
Galilée
 Théorème de Merton et mouvement accéléré mais
a mis longtemps à prendre sa forme actuelle. On observe un lien entre
analyse et géométrie en étudiant la façon dont la notion de vecteur
apparaît chez
Leibniz
Théorème de Merton et mouvement accéléré mais
a mis longtemps à prendre sa forme actuelle. On observe un lien entre
analyse et géométrie en étudiant la façon dont la notion de vecteur
apparaît chez
Leibniz
 Logique de Leibniz
au cours de ses recherches sur l'élaboration
d'un calcul des variations. Le XIXe siècle
voit l'élaboration conjointe de ce qui deviendra le produit scalaire
et de la notion de travail en
physique
Logique de Leibniz
au cours de ses recherches sur l'élaboration
d'un calcul des variations. Le XIXe siècle
voit l'élaboration conjointe de ce qui deviendra le produit scalaire
et de la notion de travail en
physique
 Grassmann et les vecteurs.
Grassmann et les vecteurs.
Le calcul vectoriel et le produit scalaire donnent une approche de la
géométrie différente de celle des Anciens, avec l'avantage de combiner
vision géométrique et
calcul
 Hamilton et les quaternions.
Hamilton et les quaternions.
Les cercles font partie des plus vieux objets
mathématiques
 Pi avant Archimède.
La caractérisation du cercle de diamètre AB comme ensemble des points
M tels que le triangle AMB soit rectangle en M semble remonter
à
Thalès
Pi avant Archimède.
La caractérisation du cercle de diamètre AB comme ensemble des points
M tels que le triangle AMB soit rectangle en M semble remonter
à
Thalès
 Théorème de Thalès et applications.
Mais ce n'est qu'au XVIIe siècle
que Descartes élabore la méthode des
coordonnées
Théorème de Thalès et applications.
Mais ce n'est qu'au XVIIe siècle
que Descartes élabore la méthode des
coordonnées
 Descartes, Fermat et les coordonnées
et écrit l'équation
d'un cercle en repère orthonormé.
Descartes, Fermat et les coordonnées
et écrit l'équation
d'un cercle en repère orthonormé.
Probabilités et statistique
Les probabilités conditionnelles peuvent être l'objet d'un travail
historique en anglais; elles apparaissent en effet dans des travaux de
Bayes
 Statistique judiciaire
et de
Moivre
Statistique judiciaire
et de
Moivre
 De Moivre et les probabilités, écrits en
anglais au XVIIIe
siècle, même si c'est
Laplace
De Moivre et les probabilités, écrits en
anglais au XVIIIe
siècle, même si c'est
Laplace
 Laplace et les probabilités
qui en a élaboré la notion. Les questions
traitées par ces auteurs peuvent parfois surprendre (exemple : quelle
est la probabilité que le soleil se lève demain, sachant qu'il s'est levé
depuis le commencement du monde ?) ; néanmoins, les probabilités
conditionnelles sont omniprésentes dans la vie courante et leur
utilisation inappropriée mène facilement à de fausses affirmations.
Laplace et les probabilités
qui en a élaboré la notion. Les questions
traitées par ces auteurs peuvent parfois surprendre (exemple : quelle
est la probabilité que le soleil se lève demain, sachant qu'il s'est levé
depuis le commencement du monde ?) ; néanmoins, les probabilités
conditionnelles sont omniprésentes dans la vie courante et leur
utilisation inappropriée mène facilement à de fausses affirmations.
L'histoire des probabilités contribue à la réflexion sur la codification
d'une théorie scientifique. On peut considérer que les origines du
« calcul des probabilités » remontent au
XVIIe siècle.
Pascal, Huygens
 Probabilités et problème des partis,
Moivre
Probabilités et problème des partis,
Moivre
 De Moivre et les probabilités,
Bernoulli
De Moivre et les probabilités,
Bernoulli
 Statistique littéraire et loi des grands nombres,
Euler, d'Alembert
Statistique littéraire et loi des grands nombres,
Euler, d'Alembert
 Paradoxe de Saint-Pétersbourg
appliquent les notions de variable aléatoire
et d'espérance à des problèmes issus de questions liées aux jeux, aux
assurances et à
l'astronomie
Paradoxe de Saint-Pétersbourg
appliquent les notions de variable aléatoire
et d'espérance à des problèmes issus de questions liées aux jeux, aux
assurances et à
l'astronomie
 Loi de Gauss, statistique et astronomie
Loi de Gauss, statistique et astronomie
 Problème des trois corps.
Problème des trois corps.
Ce n'est que vers 1930 que la description actuelle, en termes d'univers,
s'est imposée. Elle permet une formalisation souple dans laquelle
l'univers joue le rôle de « source d'aléas » .
La notion de variable aléatoire, présente sans définition précise
depuis l'origine de la discipline, apparaît alors comme une fonction
définie sur l'univers.
Algorithmique et programmation
De nombreux textes témoignent d'une préoccupation algorithmique au long
de l'Histoire
 Recettes, algorithmes et mathématiques.
Lorsqu'un texte historique a une visée
algorithmique
Recettes, algorithmes et mathématiques.
Lorsqu'un texte historique a une visée
algorithmique
 Arithmétique en Égypte
Arithmétique en Égypte
 Calculs de racines
Calculs de racines
 Triangle de Pascal
Triangle de Pascal
 Cheminement du mot algorithme
Cheminement du mot algorithme
 Comput pascal
transformer les méthodes qu'il présente en un algorithme, voire en un
programme, ou inversement, est l'occasion de travailler des changements
de registre qui donnent du sens au formalisme mathématique.
Comput pascal
transformer les méthodes qu'il présente en un algorithme, voire en un
programme, ou inversement, est l'occasion de travailler des changements
de registre qui donnent du sens au formalisme mathématique.
Numérique et sciences informatiques
Comme toute connaissance scientifique et technique, les concepts de
l'informatique ont une histoire et ont été forgés par des personnes.
Les algorithmes sont présents dès l'Antiquité
 Recettes, algorithmes et mathématiques
Recettes, algorithmes et mathématiques
 Cheminement du mot algorithme,
les machines à calculer apparaissent progressivement au XVIIe siècle
Cheminement du mot algorithme,
les machines à calculer apparaissent progressivement au XVIIe siècle
 Cylindre à picots
Cylindre à picots
 Machines à calculer
Machines à calculer
 Automates de Vaucanson
Automates de Vaucanson
 Calcul analogique,
les sciences de l'information sont fondées au XIXe siècle
Calcul analogique,
les sciences de l'information sont fondées au XIXe siècle
 Babbage et l'invention de l'ordinateur
Babbage et l'invention de l'ordinateur
 La vision d'Ada Lovelace,
mais c'est en 1936 qu'apparaît le concept de machine
universelle
La vision d'Ada Lovelace,
mais c'est en 1936 qu'apparaît le concept de machine
universelle
 Leibniz, précurseur de l'informatique,
capable d'exécuter tous les algorithmes, et que les notions de
machine, algorithme, langage et information sont pensées comme un tout
cohérent
Leibniz, précurseur de l'informatique,
capable d'exécuter tous les algorithmes, et que les notions de
machine, algorithme, langage et information sont pensées comme un tout
cohérent
 Torres y Quevedo entre Babbage et Turing
Torres y Quevedo entre Babbage et Turing
 Intelligence artificielle.
Les premiers ordinateurs ont été construits en
1948
Intelligence artificielle.
Les premiers ordinateurs ont été construits en
1948
 Premiers ordinateurs
Premiers ordinateurs
 Calcul au début des ordinateurs
et leur puissance a ensuite évolué exponentiellement. Parallèlement,
les ordinateurs se sont diversifiés dans leur taille, leur forme et
leur emploi : téléphones, tablettes, montres connectées, ordinateurs
personnels, serveurs, fermes de calcul, méga-ordinateurs. Le réseau
internet, développé depuis 1969, relie aujourd'hui ordinateurs et
objets connectés.
Calcul au début des ordinateurs
et leur puissance a ensuite évolué exponentiellement. Parallèlement,
les ordinateurs se sont diversifiés dans leur taille, leur forme et
leur emploi : téléphones, tablettes, montres connectées, ordinateurs
personnels, serveurs, fermes de calcul, méga-ordinateurs. Le réseau
internet, développé depuis 1969, relie aujourd'hui ordinateurs et
objets connectés.
Terminale ►
Algèbre et géométrie
Véritable porte d'entrée sur l'infini
 L'infini mathématique,
le raisonnement par récurrence
L'infini mathématique,
le raisonnement par récurrence
 Induction et récurrence
a été formalisé comme principe de raisonnement par Pascal, et surtout par
Peano
Induction et récurrence
a été formalisé comme principe de raisonnement par Pascal, et surtout par
Peano
 Symbolisme et axiomes de Peano et
ses collaborateurs et avait été anticipé comme mode de démonstration par les
mathématiciens anciens (nombres latéraux et diagonaux
Symbolisme et axiomes de Peano et
ses collaborateurs et avait été anticipé comme mode de démonstration par les
mathématiciens anciens (nombres latéraux et diagonaux
 Pythagore : religion et arithmétique),
médiévaux (al-Karaji,
As-Samawal, Fibonacci) et renaissants (Maurolico).
Pythagore : religion et arithmétique),
médiévaux (al-Karaji,
As-Samawal, Fibonacci) et renaissants (Maurolico).
Des propriétés arithmétiques du Triangle de
Pascal
 Triangle de Pascal étaient
présentes dans les
travaux combinatoires des mathématiques
indiennes
Triangle de Pascal étaient
présentes dans les
travaux combinatoires des mathématiques
indiennes
 Poètes et mathématiciens en Inde
et chinoises. La
combinatoire
Poètes et mathématiciens en Inde
et chinoises. La
combinatoire
 Combinatoire d'un vers latin
était un objet de prédilection des récréations mathématiques dès
l'Antiquité
Combinatoire d'un vers latin
était un objet de prédilection des récréations mathématiques dès
l'Antiquité
 Énigmes algébriques et fausse position et
est encore présente chez des arithméticiens du XIXe
siècle (Lucas, Delannoy, Laisant
Énigmes algébriques et fausse position et
est encore présente chez des arithméticiens du XIXe
siècle (Lucas, Delannoy, Laisant
 Mathématiques amusantes, selon Lucas et Laisant).
Il est par ailleurs pertinent de souligner le développement récent des « mathématiques discrètes », motivé notamment
par l'informatique et l'intelligence artificielle
Mathématiques amusantes, selon Lucas et Laisant).
Il est par ailleurs pertinent de souligner le développement récent des « mathématiques discrètes », motivé notamment
par l'informatique et l'intelligence artificielle
 Intelligence artificielle
.
Intelligence artificielle
.
Les concepts sous-jacents à la notion de
vecteur
 Grassmann et les vecteurs
apparaissent comme modèles
physiques dynamiques longtemps avant leur formalisation. On trouve un concept
de force et la composition des forces chez Newton; ces notions, comme celles
de vitesse, sont présentes dans le calcul géométrique de Leibniz.
Grassmann et les vecteurs
apparaissent comme modèles
physiques dynamiques longtemps avant leur formalisation. On trouve un concept
de force et la composition des forces chez Newton; ces notions, comme celles
de vitesse, sont présentes dans le calcul géométrique de Leibniz.
Au XIXe siècle, la notion de vecteur va émerger
comme objet algébrique et géométrique, comme transformation ou comme outil
de repérage. Hamilton construit les vecteurs par une approche
algébrique
 Hamilton et les quaternions.
Dans sa théorie des forces et des marées de 1839,
Grassmann
Hamilton et les quaternions.
Dans sa théorie des forces et des marées de 1839,
Grassmann
 Grassmann et les vecteurs
propose une approche géométrique qui étend à l'espace la notion de
vecteur et lui associe des règles de calcul algébrique, notamment un « produit linéaire »
utilisant la projection orthogonale et qui deviendra notre produit scalaire.
À la fin du siècle, des auteurs proches des mathématiques comme de la physique
(Maxwell, Gibbs, Heaviside ou Peano) dégagent les principes du calcul
vectoriel à trois dimensions ou plus, lui donnant une dimension dynamique
tout en établissant la structure d'espace vectoriel.
Grassmann et les vecteurs
propose une approche géométrique qui étend à l'espace la notion de
vecteur et lui associe des règles de calcul algébrique, notamment un « produit linéaire »
utilisant la projection orthogonale et qui deviendra notre produit scalaire.
À la fin du siècle, des auteurs proches des mathématiques comme de la physique
(Maxwell, Gibbs, Heaviside ou Peano) dégagent les principes du calcul
vectoriel à trois dimensions ou plus, lui donnant une dimension dynamique
tout en établissant la structure d'espace vectoriel.
Analyse
Le calcul infinitésimal, qui contient les fonctions usuelles, le calcul différentiel et intégral ont historiquement précédé la notion de limite qui en donnera des fondements rigoureux.
On trouve des anticipations du calcul intégral chez
Archimède
 Quadratures d'Archimède
(longueur du cercle, quadrature de la
parabole
Quadratures d'Archimède
(longueur du cercle, quadrature de la
parabole
 Thabit ibn Qurra et l'analyse,
cubature des solides), Liu-Hui (volume
d'un cylindre), Ibn al-Haytham
Thabit ibn Qurra et l'analyse,
cubature des solides), Liu-Hui (volume
d'un cylindre), Ibn al-Haytham
 Kepler et le calcul intégral
(volume d'un paraboloïde) puis, bien plus tard,
chez Grégoire de Saint-Vincent
Kepler et le calcul intégral
(volume d'un paraboloïde) puis, bien plus tard,
chez Grégoire de Saint-Vincent
 Paradoxes de Zénon et séries géométriques
(méthode d'exhaustion) ou encore chez Galilée
ou Cavalieri
Paradoxes de Zénon et séries géométriques
(méthode d'exhaustion) ou encore chez Galilée
ou Cavalieri
 Pascal et la cycloïde
Pascal et la cycloïde
 Kepler et le calcul intégral
(méthode des indivisibles).
Kepler et le calcul intégral
(méthode des indivisibles).
Les procédés par lesquels les mathématiciens ont construit et tabulé le
logarithme
 Napier et les logarithmes
et les fonctions trigonométriques
Napier et les logarithmes
et les fonctions trigonométriques
 Premières tables trigonométriques
Premières tables trigonométriques
 Des cordes à la sinusoïde
illustrent les liens entre
discret et continu et fournissent une source féconde d'activités. On peut
mentionner les méthodes de Ptolémée et d'Al-Kashi
Des cordes à la sinusoïde
illustrent les liens entre
discret et continu et fournissent une source féconde d'activités. On peut
mentionner les méthodes de Ptolémée et d'Al-Kashi
 Théorème d'al-Kashi,
la méthode de Briggs ou
l'utilisation de développements en
série
Théorème d'al-Kashi,
la méthode de Briggs ou
l'utilisation de développements en
série
 Newton et l'analyse numérique
Newton et l'analyse numérique
 Newton et l'analyse infinitésimale
Newton et l'analyse infinitésimale
 Newton contre Leibniz.
Ces travaux, dont certains ont été
anticipés hors d'Europe, par exemple en Inde par l'école du
Kerala
Newton contre Leibniz.
Ces travaux, dont certains ont été
anticipés hors d'Europe, par exemple en Inde par l'école du
Kerala
 Développements en série, indiquent
une perception intuitive claire des questions de convergence.
Développements en série, indiquent
une perception intuitive claire des questions de convergence.
Le calcul différentiel s'est développé de concert avec la physique mathématique
au XVIIe siècle. Parmi les initiateurs,
Fermat
 Optimisation selon Fermat,
Huygens
Optimisation selon Fermat,
Huygens
 Détermination des longitudes,
Pascal
Détermination des longitudes,
Pascal
 Pascal et la cycloïde et
Barrow
Pascal et la cycloïde et
Barrow
 Newton et l'analyse infinitésimale
reconnaissent que le problème des aires (le calcul
intégral) est le problème inverse de celui des tangentes (la dérivation) ; ce
thème peut être abordé à partir des travaux sur la quadrature de
l'hyperbole
Newton et l'analyse infinitésimale
reconnaissent que le problème des aires (le calcul
intégral) est le problème inverse de celui des tangentes (la dérivation) ; ce
thème peut être abordé à partir des travaux sur la quadrature de
l'hyperbole
 Paradoxes de Zénon et séries géométriques.
Paradoxes de Zénon et séries géométriques.
Les travaux de Newton et Leibniz révèlent deux visions et deux pratiques
différentes du calcul infinitésimal
 Newton contre Leibniz.
La justification de telles méthodes
nécessitait une mise au point de la notion de
limite
Newton contre Leibniz.
La justification de telles méthodes
nécessitait une mise au point de la notion de
limite
 Oppositions au calcul différentiel
Oppositions au calcul différentiel
 Cordes vibrantes.
Des fondations solides sont proposées dans le Cours d'Analyse de
Cauchy
Cordes vibrantes.
Des fondations solides sont proposées dans le Cours d'Analyse de
Cauchy
 Bolzano, Cauchy et la rigueur
Bolzano, Cauchy et la rigueur
 Série du binôme de Newton
Série du binôme de Newton
 Cauchy et la variable complexe
(1821, 1823), qui définit
précisément la notion de limites et en fait le point de départ de l'analyse.
Parallèlement, les résolutions d'équations différentielles, provenant de la
mécanique ou des mathématiques elles-mêmes, se structurent notamment en lien
avec les séries (Newton, Euler, D'Alembert, Lagrange, Cauchy, Clairaut,
Riccati
Cauchy et la variable complexe
(1821, 1823), qui définit
précisément la notion de limites et en fait le point de départ de l'analyse.
Parallèlement, les résolutions d'équations différentielles, provenant de la
mécanique ou des mathématiques elles-mêmes, se structurent notamment en lien
avec les séries (Newton, Euler, D'Alembert, Lagrange, Cauchy, Clairaut,
Riccati
 Newton et l'analyse infinitésimale
Newton et l'analyse infinitésimale
 Newton contre Leibniz
Newton contre Leibniz
 Les Bernoulli et l'analyse
Les Bernoulli et l'analyse
 Fenêtre de Viviani)
et illustrent là encore les ponts entre le discret et le continu.
Fenêtre de Viviani)
et illustrent là encore les ponts entre le discret et le continu.
Probabilités
La parution de l'Ars Conjectandi de J. Bernoulli
 Statistique littéraire et loi des grands nombres
(1713), reprenant notamment d'anciens travaux de Huygens
Statistique littéraire et loi des grands nombres
(1713), reprenant notamment d'anciens travaux de Huygens
 Probabilités et problème des partis,
marque une rupture dans l'histoire des probabilités. On y trouve la
première étude de la distribution binomiale,
introduite dans le cadre d'un tirage sans remise pour un modèle d'urne
Probabilités et problème des partis,
marque une rupture dans l'histoire des probabilités. On y trouve la
première étude de la distribution binomiale,
introduite dans le cadre d'un tirage sans remise pour un modèle d'urne
 Statistique littéraire et loi des grands nombres.
Statistique littéraire et loi des grands nombres.
Un résultat majeur de cet ouvrage est son «
théorème d'or », la loi des
grands nombres, qui relie fréquences et probabilité, valide le principe de
l'échantillonnage et est le premier exemple de « théorème limite » en
théorie des probabilités. Le mathématicien français Bienaymé (en 1853,
publication en 1867) et le mathématicien russe Tchebychev (en 1867) démontrent
l'inégalité qui porte leur nom, en parlant de fréquences d'échantillons plutôt
que de variables aléatoires. Ils fournissent ainsi la possibilité d'une
démonstration plus simple de la loi des grands
nombres
 De Moivre et les probabilités.
De Moivre et les probabilités.
Au début du XIXe siècle, la modélisation des
erreurs de mesure va devenir centrale pour faire de la statistique une science
à part entière. Lagrange et Laplace développent une approche probabiliste de
la théorie des erreurs. Gauss (1809, 1821), après Legendre (1805), imagine
une méthode des moindres
carrés
 Loi de Gauss, statistique et astronomie
Loi de Gauss, statistique et astronomie
 Problème des trois corps
qu'il applique avec succès à la prédiction
de la position d'un astéroïde. Il y propose de comprendre l'écart-type comme
une « erreur moyenne à craindre ».
Problème des trois corps
qu'il applique avec succès à la prédiction
de la position d'un astéroïde. Il y propose de comprendre l'écart-type comme
une « erreur moyenne à craindre ».
L'introduction de méthodes statistiques en sociologie est l'œuvre du
mathématicien et astronome belge Quetelet
 Statistiques démographiques
Statistiques démographiques
 Statistique littéraire et loi des grands nombres
dans les années 1830. Il réfléchit
à la distribution de données autour de la moyenne, ce qui sera approfondi
notamment par l'Anglais Galton
Statistique littéraire et loi des grands nombres
dans les années 1830. Il réfléchit
à la distribution de données autour de la moyenne, ce qui sera approfondi
notamment par l'Anglais Galton
 Statistique et eugénisme.
Statistique et eugénisme.
Algorithmique et programmation
De nombreux textes témoignent d'une préoccupation algorithmique au long
de l'Histoire
 Recettes, algorithmes et mathématiques.
Lorsqu'un texte historique a une visée algorithmique
Recettes, algorithmes et mathématiques.
Lorsqu'un texte historique a une visée algorithmique
 Arithmétique en Égypte
Arithmétique en Égypte
 Calculs de racines
Calculs de racines
 Triangle de Pascal
Triangle de Pascal
 Cheminement du mot algorithme
Cheminement du mot algorithme
 Comput pascal
transformer les méthodes qu'il présente en un algorithme, voire en un
programme, ou inversement, est l'occasion de travailler des changements
de registre qui donnent du sens au formalisme mathématique.
Comput pascal
transformer les méthodes qu'il présente en un algorithme, voire en un
programme, ou inversement, est l'occasion de travailler des changements
de registre qui donnent du sens au formalisme mathématique.
Nombres complexes
L'algèbre s'est longtemps identifiée à l'étude des équations polynomiales.
La recherche de formules pour les racines analogues à celles du second degré
a constitué un problème central chez les mathématiciens italiens de la
Renaissance, notamment Tartaglia, Cardan
 Équations de degré trois,
Bombelli
Équations de degré trois,
Bombelli
 Algebre de Bombelli,
ou encore chez Descartes
Algebre de Bombelli,
ou encore chez Descartes
 Descartes, Fermat et les coordonnées
ou Girard
Descartes, Fermat et les coordonnées
ou Girard
 Stevin, Girard et l'algèbre avant Descartes,
chez qui on voit apparaître des quantités complexes
sous forme symbolique. Ces textes révèlent l'importance des notations en
mathématiques
Stevin, Girard et l'algèbre avant Descartes,
chez qui on voit apparaître des quantités complexes
sous forme symbolique. Ces textes révèlent l'importance des notations en
mathématiques
 Galois, Abel, et le cinquième degré ;
ils soulignent la différence entre formules de résolution
symbolique et méthodes d'approximation. Ils montrent aussi que la découverte
de nouveaux objets mathématiques ne passe pas par les chemins qui semblent
rétrospectivement les plus directs.
Galois, Abel, et le cinquième degré ;
ils soulignent la différence entre formules de résolution
symbolique et méthodes d'approximation. Ils montrent aussi que la découverte
de nouveaux objets mathématiques ne passe pas par les chemins qui semblent
rétrospectivement les plus directs.
La réalisation géométrique des nombres complexes
 Représentation géométrique des complexes
apparaît plus tard chez Gauss
Représentation géométrique des complexes
apparaît plus tard chez Gauss
 Gauss et l'arithmétique complexe,
Argand ou Mourey, où l'on trouve un lien entre les nombres complexes
et la tentative de formaliser ce qui deviendra les vecteurs. Une
illustration de l'efficacité de ce lien entre calcul et géométrie est
le calcul de cos(pi/5), qu'on peut mettre en perspective avec la
construction du pentagone
régulier dans les Éléments d'Euclide
Gauss et l'arithmétique complexe,
Argand ou Mourey, où l'on trouve un lien entre les nombres complexes
et la tentative de formaliser ce qui deviendra les vecteurs. Une
illustration de l'efficacité de ce lien entre calcul et géométrie est
le calcul de cos(pi/5), qu'on peut mettre en perspective avec la
construction du pentagone
régulier dans les Éléments d'Euclide
 Le nombre d'or
Le nombre d'or
 Premières tables trigonométriques
Premières tables trigonométriques
 Solution des trois problèmes grecs.
Klein introduit, dans son programme d'Erlangen
Solution des trois problèmes grecs.
Klein introduit, dans son programme d'Erlangen
 Klein et son programme d'Erlangen,
un point de vue sur
la géométrie qui transparaît dans l'étude des similitudes directes
du plan complexe.
Klein et son programme d'Erlangen,
un point de vue sur
la géométrie qui transparaît dans l'étude des similitudes directes
du plan complexe.
Les nombres complexes, introduits pour des raisons internes aux mathématiques, sont désormais des outils importants en physique (électricité notamment) et économie (cycle de croissance, de prix).
Arithmétique
L'arithmétique des entiers est présente chez les mathématiciens grecs,
par exemple dans les Éléments d'Euclide
 Recettes, algorithmes et mathématiques,
chez Nicomaque de Gérase
Recettes, algorithmes et mathématiques,
chez Nicomaque de Gérase
 Pythagore : religion et arithmétique
Pythagore : religion et arithmétique
 Boèce et ses mathématiques
Boèce et ses mathématiques
 Arithmétique arabe,
Théon de Smyrne
Arithmétique arabe,
Théon de Smyrne
 Aristote et l'arithmétique
ou encore Diophante
Aristote et l'arithmétique
ou encore Diophante
 Arithmétiques de Diophante,
dont certains développements touchent à la combinatoire
Arithmétiques de Diophante,
dont certains développements touchent à la combinatoire
 Équation de Pell-Fermat.
Les aspects algorithmiques sont présents depuis l'origine : méthodes de fausse
position
Équation de Pell-Fermat.
Les aspects algorithmiques sont présents depuis l'origine : méthodes de fausse
position
 Énigmes algébriques et fausse position
Énigmes algébriques et fausse position
 Arithmétiques commerciales
Arithmétiques commerciales
 Systèmes d'équations en Chine,
algorithme d'Euclide
Systèmes d'équations en Chine,
algorithme d'Euclide
 Recettes, algorithmes et mathématiques
Recettes, algorithmes et mathématiques
 Algèbre indienne
Algèbre indienne
 Astronomie indienne,
algorithme d'Euclide étendu de Bachet (1612)
Astronomie indienne,
algorithme d'Euclide étendu de Bachet (1612)
 Récréations mathématiques
puis Bézout (1766), applications aux fractions
continues
Récréations mathématiques
puis Bézout (1766), applications aux fractions
continues
 Calculs de racines
chez Euler (1737)
Calculs de racines
chez Euler (1737)
 Astronomie indienne,
nombre de racines d'une équation chez Sturm
Astronomie indienne,
nombre de racines d'une équation chez Sturm
 Localisation des racines d'équations (1835).
Localisation des racines d'équations (1835).
 Fermat et l'arithmétique,
Lagrange
Fermat et l'arithmétique,
Lagrange
 Le repos philosophique de Lagrange,
Gauss
Le repos philosophique de Lagrange,
Gauss
 Gauss et l'arithmétique complexe,
Dirichlet
Gauss et l'arithmétique complexe,
Dirichlet
 Séries trigonométriques
et de bien d'autres
Séries trigonométriques
et de bien d'autres
 Hadamard, Erdös et les nombres premiers,
fourmille de théorèmes d'énoncés simples aux preuves difficiles
Hadamard, Erdös et les nombres premiers,
fourmille de théorèmes d'énoncés simples aux preuves difficiles
 Théorème de Fermat, de Kummer à Wiles,
ainsi que de conjectures de formulation élémentaire mais non résolues.
Théorème de Fermat, de Kummer à Wiles,
ainsi que de conjectures de formulation élémentaire mais non résolues.
Des questions issues de l'arithmétique, apparemment gratuites, ont donné
lieu à des applications spectaculaires en
cryptographie
 Machines cryptographiques
ou codage. On
peut noter enfin l'intérêt historique de l'étude de nombres particuliers
par exemple ceux de Fermat
Machines cryptographiques
ou codage. On
peut noter enfin l'intérêt historique de l'étude de nombres particuliers
par exemple ceux de Fermat
 Fermat et l'arithmétique,
Mersenne, Carmichael ou Sophie Germain
Fermat et l'arithmétique,
Mersenne, Carmichael ou Sophie Germain
 Sophie Germain et ses mathématiques.
Sophie Germain et ses mathématiques.
Graphes et matrices
L'histoire de cette partie combine trois thèmes très contemporains :
les graphes, outils fondamentaux des mathématiques discrètes, les matrices
 Sylvester, Cayley et les matrices
et les chaînes de
Markov
Sylvester, Cayley et les matrices
et les chaînes de
Markov
 Proportion des voyelles.
Les liens mis en évidence soulignent l'unité
et l'efficacité des mathématiques.
Proportion des voyelles.
Les liens mis en évidence soulignent l'unité
et l'efficacité des mathématiques.
L'histoire des graphes remonte au moins à Euler, par exemple à travers
le problème des ponts de Königsberg. Des applications plus récentes
en intelligence artificielle, concernant notamment les réseaux, soulignent
la pertinence et l'actualité de la modélisation à l'aide de graphes et
matrices
 Valeurs propres.
Valeurs propres.
Numérique et sciences informatiques
Comme toute connaissance scientifique et technique, les concepts de
l'informatique ont une histoire et ont été forgés par des personnes.
Les algorithmes sont présents dès l'Antiquité
 Recettes, algorithmes et mathématiques
Recettes, algorithmes et mathématiques
 Calculs de racines
Calculs de racines
 Cheminement du mot algorithme
Cheminement du mot algorithme
 Comput pascal,
les machines à calculer
apparaissent progressivement au XVIIe siècle
Comput pascal,
les machines à calculer
apparaissent progressivement au XVIIe siècle
 Cylindre à picots
Cylindre à picots
 Machines à calculer
Machines à calculer
 Automates de Vaucanson
Automates de Vaucanson
 Calcul analogique,
les sciences de l'information sont fondées au XIXe siècle
Calcul analogique,
les sciences de l'information sont fondées au XIXe siècle
 Babbage et l'invention de l'ordinateur
Babbage et l'invention de l'ordinateur
 La vision d'Ada Lovelace,
mais c'est en 1936 qu'apparaît le concept de machine universelle
La vision d'Ada Lovelace,
mais c'est en 1936 qu'apparaît le concept de machine universelle
 Leibniz, précurseur de l'informatique,
capable d'exécuter tous les algorithmes, et que les notions de
machine, algorithme, langage et information sont pensées comme un tout
cohérent
Leibniz, précurseur de l'informatique,
capable d'exécuter tous les algorithmes, et que les notions de
machine, algorithme, langage et information sont pensées comme un tout
cohérent
 Torres y Quevedo entre Babbage et Turing
Torres y Quevedo entre Babbage et Turing
 Intelligence artificielle.
Les premiers ordinateurs ont été construits en
1948
Intelligence artificielle.
Les premiers ordinateurs ont été construits en
1948
 Premiers ordinateurs
Premiers ordinateurs
 Calcul au début des ordinateurs
et leur puissance a ensuite évolué exponentiellement. Parallèlement,
les ordinateurs se sont diversifiés dans leur taille, leur forme et
leur emploi : téléphones, tablettes, montres connectées, ordinateurs
personnels, serveurs, fermes de calcul, méga-ordinateurs. Le réseau
internet, développé depuis 1969, relie aujourd'hui ordinateurs et
objets connectés.
Calcul au début des ordinateurs
et leur puissance a ensuite évolué exponentiellement. Parallèlement,
les ordinateurs se sont diversifiés dans leur taille, leur forme et
leur emploi : téléphones, tablettes, montres connectées, ordinateurs
personnels, serveurs, fermes de calcul, méga-ordinateurs. Le réseau
internet, développé depuis 1969, relie aujourd'hui ordinateurs et
objets connectés.